Monochrome pixel graphics

Little black squares

This is the third step of the introduction to the nightmare that is realtime graphics coding for the HP48 calculator and now i'll try explaining how pixel graphics work.

The display is 131 pixels (little squares) wide and 64 pixels high. Well, actually the display is 136 pixels wide, but the rightmost 5 pixels are not there. We still have to take them into account when programming, but the player will never see them.

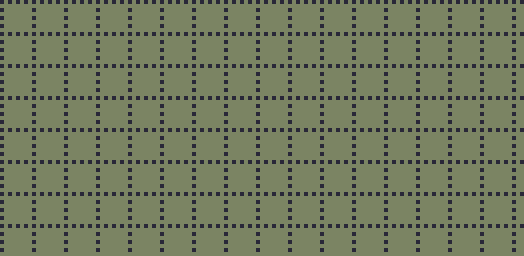The display

In the above image, most pixels are some sickly shade of green, but some pixels (the grid pattern) are very dark blue. I show you this grid so you can see the resolution and scale of the display. The dark blue pixels are "on" and the green are "off". On a more common display, they would be respectively black (off) and white (on). We will rarely see anything "common" applicable to this calculator. 

Now focus on this square of 16 pixels:

Some pixels

(The black grid is not part of the display, it's there only so you can tell how the individual pixels are divided.)

Let's assign the digit 0 for each pixel that is off (green) and the digit 1 for each pixel that is on (dark blue). The above square can be thus represented with the following sequence of lines:

0001

0000

1111

0000

But if we interpret the sequence "0001" as a binary number, it represents the quantity "one". Similarly, the other three lines represent the quantities 0, 15 and 0, in decimal notation, the notation you use daily. In hexadecimal notation, they are the numbers 1, 0, F and 0.

This method is important because it means we can represent an image with numbers.  Just take it one row at a time, divide each row into sets of four pixels, "read" those sets them from left to right, represent each four pixels with one number from 0 to 15 and write them down. The first row on the larger, first, image above (The display) would be 34 repetitions (because 34*4=136) of 10, the second row would be 34 repetitions of 0 (because the row has only pixels in the "off" state) and the third row would be the pattern 8, 0 repeated 17 times. That is, of course, in decimal. In hexadecimal, and writing each row sequentially, it would be writen ("stored in memory") as:

AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA00000000000000000000000000000000008080808080808080808080808080808080

, with each digit (number) stored in each memory location and in increasing order (what, you thought memory is organized in bytes? Hahahaha, no. Half bytes, or nibbles). Thankfully, we don't have to mess with such cumbersome representations of memory, we mostly consider the display divided into tiles, such as the grid in the first picture, which is the 8-by-8-pixel tile:

AA

00

80

00

80

00

80

00

, repeated in specific locations in memory (not all sequentially).

That representation is somewhat easier to imagine, even if it doesn't always correspond directly to what exists in memory. An all black, 4-by-4 square would be FFFF. All white, 0000. Checkerboard pattern, A5A5.

The following picture shows all possible patters represented with the numbers 0 to 15 (decimal) or 0 to F (hexadecimal), from top to bottom.

All numbers

In other words, how each number, from 0 to F, is shown on screen.

The conclusion is: if we want to display a character on the screen, we have to take the image:

Duuh...

, divide it into sets of 4 pixels in a row, find out what numbers correspond to each pattern and write those numbers to the appropriate memory locations. In the case of our perplexed friend above, the pattern of the first (=leftmost) four pixels of the first row corresponds to the fourth row in the previous image, the row which shows how the number three (the first line shows the number zero) appears on screen. Another way is considering the pixels in sets of four, as binary digits (0011) and reading them as hex digits (3). First row: 0011, 1111, 1111, 0000 or 3,F,F,0. Second row, 400C, etc.

Thanks for reading. More, later.